I recently had the pleasure of being part of a panel discussion at the American Philosophical Association with Joe Schmid and Alex Pruss. We talked about causal finitism, the thesis that all causal chains are finite. My contribution involved offering a new formulation of the grim reaper paradox in terms of an infinite sequence of Liar sentences that resists classical solutions. I present a summary of my APA handout here.
A Formula for Paradox
Here’s a simple recipe for paradox:
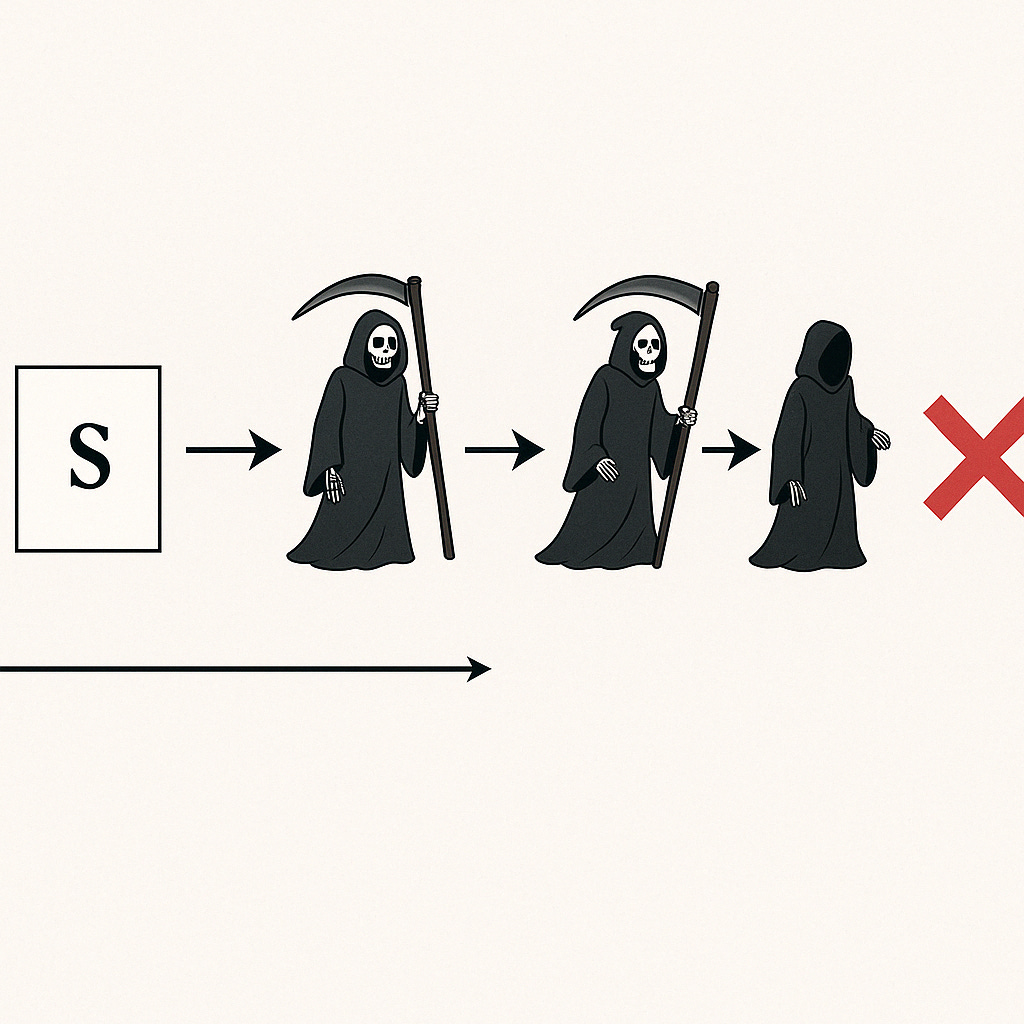
Start with a scenario, S, that seems possible—or at least not obviously impossible.
Apply a principle of recombination: if S is possible, then a further scenario, Q, is possible.
But suppose Q leads to a contradiction.
Then S must not be possible after all.
This pattern helps us test the limits of possibility by seeing what follows from recombining elements in different ways. But some recombinations lead to trouble. Let’s look at two cases.
Case A: The Liar Scenario
Take the sentence:
“There is no true sentence next to this sentence.”
This seems intelligible. It could even be true.
But now imagine putting it next to the sentence “There is a true sentence next to this one.” What happens? Each sentence is true if and only if the other is not. That’s a contradiction. So something has gone wrong.
But notice: the problem isn’t with spatial recombination. We can put words next to each other all day. The issue runs deeper.
Enter the Truthmaking Hypothesis:
A sentence is true if and only if there exists a truthmaker—a state of affairs that makes the sentence true—which is explanatorily prior to the sentence itself.
This hypothesis helps explain why the paradox emerges. When a sentence is created, it “scans” reality to see if anything would make that sentence true. If something makes it true, then it is true. If not, then the sentence is false. This account solves the classical liar puzzle because the liar sentence fails to correspond to any truthmaker that existed prior to the existence of that very sentence. Hence, the liar sentence is simply false—and there’s no problem.
Case B: Infinite Liars
But now consider this variation. Let the sentence S be:
“There has never been a true sentence.”
S is clearly false, since there have been true sentences. But now imagine that every day from eternity past, a new copy of S is created. Suppose these are the only sentences that ever exist.
Is any copy of S true?
Well, one is true if and only if none are true. That’s a contradiction.
This contradiction parallels the famous Grim Reaper Paradox. Suppose you have an infinite sequence of Grim Reapers, each poised to kill Fred if and only if no earlier Reaper has already done so. Does any Reaper kill Fred? Yes—if and only if not. Again, a contradiction.
The Root of the Problem
These paradoxes arise from setups that implement this condition:
X if and only if not-X
But what enables such setups? The root problem seems to vary from case to case. In the first case, we solved the problem with a Truthmaking Hypothesis. However, that hypothesis doesn’t solve the second case, for the contradiction still emerges if we grant the Truthmaking Hypothesis. Indeed, the Truthmaking Hypothesis is part of what generates the paradox here, since each token of S would already have its truthmaker in place, either to make that token true or not true.
So what’s the real root?
The Infinite Root Hypothesis
Here’s the idea:
If an infinite regress of causally dependent events is possible, then paradoxical setups like “X iff not-X” can be implemented.
This principle is supported by a recombination principle, whereby any instance of any sentence could exist at any time, since the existence of one sentence is independent from the existence of others. Note that once more, the problem is not with recombination (according to this proposal) but with another part of the setup.
Of course, the paradoxical setup is impossible. Therefore, an infinite regress of causal events is not possible.
This gives us an argument for causal finitism—the view that the causal chain of past events must have a beginning.
A Brief Argument for Causal Finitism
Suppose there could be an infinite sequence of causally dependent past events.
Then a paradoxical setup like “X iff not-X” could be implemented (by the Infinite Root Hypothesis).
But such a setup is impossible.
Therefore, the past cannot contain an infinite sequence of causally dependent events.
A place to further explore involves probing motivations for and against (2). For example, are there parodies or extensions of (2) that have untoward implications? That’s what I’m still thinking about.